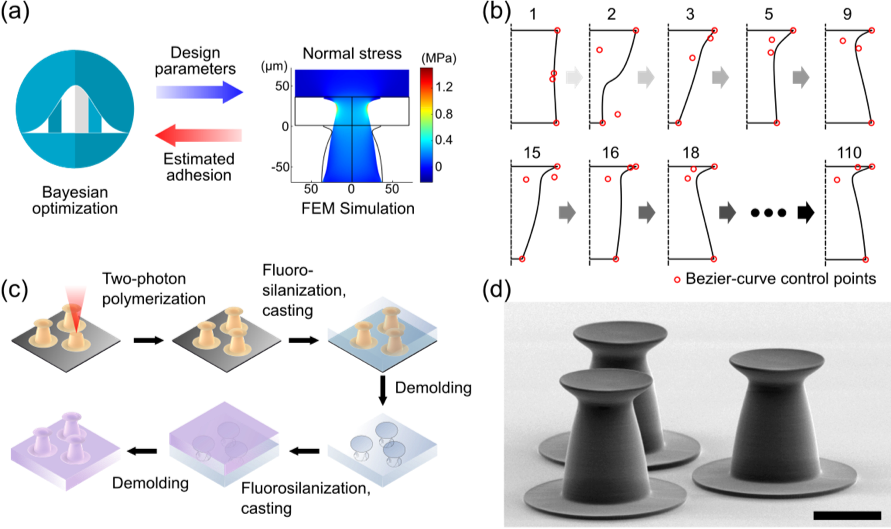
Design and fabrication process of the machine learning-based design of fibrils for maximal adhesion on smooth flat surfaces. A) A design optimization goal (e.g., maximize adhesion) along with the design constraints is supplied to the Bayesian optimization algorithm. The Bayesian optimizer provides design parameters to the simulator, and the simulator returns the estimated adhesion back using a finite element method (FEM)-based adhesion mechanics simulation. This process runs iteratively until the optimal design is achieved. B) The algorithm starts with a random shape and explores the broad design space by controlling Bezier-curve control points to maximize the estimated adhesive force from the FEM simulation. In each iteration, a comprehensive FEM simulation from the initial attachment to the detachment is performed. As the iteration number increases, the shape evolves to the best design. C) After the optimization, the best design is fabricated using two-photon polymerization and a subsequent double molding-based replication technique. D) The fabricated version of the optimal fibril design with the tip diameter of 70 µm (iteration number 110) is shown in a scanning electron microscope image (scale bar: 50 µm).
Objective of the project is to develop a machine learning technique to design optimal shape of adhesive fibril shapes [ ]. Designing dry fibrillar adhesives is limited by a template-based design-approach using a pre-determined bioinspired T- or wedge-shaped mushroom tips. Here, we show a machine learning-based computational approach to optimize designs of adhesive fibrils, exploring a much broader design space. A combination of Bayesian optimization and finite element methods creates novel optimal designs of adhesive fibrils, which are fabricated by two-photon-polymerization-based 3D microprinting and double-molding-based replication out of PDMS. Such optimal elastomeric fibril designs outperform previously proposed designs by maximum 77% in the experiments of dry adhesion performance on smooth surfaces. Furthermore, finite-element analyses reveal that the adhesion of the fibrils is sensitive to the 3D fibril stem shape, tensile deformation, and fibril microfabrication limits, which contrast with the previous assumptions that mostly neglect the deformation of the fibril tip and stem, and focus only on the fibril tip geometry. The proposed computational fibril design could help design future optimal fibrils for different specific applications with less help from the human intuition.
